يولي لونكانغ “لوكا” لي، طالب الدكتوراه في قسم تعلم الآلة بجامعة محمد بن زايد للذكاء الاصطناعي، اهتماماً خاصاً بمجال اكتشاف العلاقات السببية، وهو المجال الذي يهدف إلى تحديد العلاقات السببية بين المتغيّرات بالاعتماد على البيانات وشرح كيفية تأثير الأشياء في العالم بعضها في بعض.

يؤثر اكتشاف العلاقات السببية على مجموعة واسعة من التخصصات الأخرى، مثل علم الأحياء والاقتصاد والصحة العامة، حيث قد تكون التجارب إما مرتفعة التكلفة، أو تستغرق وقتاً طويلاً، أو لا يمكن تنفيذها بشكل يوضح العلاقات السببية. ورغم توافر بيانات قابلة للملاحظة في هذه المجالات، مثل البيانات الاقتصادية التي تنشرها الحكومات أو بيانات التجارب السريرية، فإن هذه البيانات بمفردها لا توفّر كثيراً من المعلومات عن العلاقات السببية.

وتعد هذه هي العقبة التي يواجهها العلماء الذين يعملون في مجال اكتشاف العلاقات السببية، أي تحديد العلاقات السببية في مجموعات بيانات ضخمة ومعقدة بهدف فهم كيفية عمل الأشياء. ويعلّق لي على ذلك بقوله: “عالمنا مليء بالفوضى والألغاز، ولكن يمكننا دائماً إيجاد طريقة لاكتشاف الحقيقة وإحداث التغييرات المرغوبة”.

أعد لي، بالاشتراك مع زملاء له من جامعة محمد بن زايد للذكاء الاصطناعي ومؤسسات أخرى، دراسة تقترح طريقة جديدة لتحديد العلاقات بين ما يُسمّى المتغيّرات الحتمية والمتغيّرات غير الحتمية. وقدّم الفريق نتائج الدراسة في المؤتمر السنوي الثامن والثلاثين لنظم معالجة المعلومات العصبية الذي عُقد في فانكوفر.

الآثار العملية

يهتم لي بكيفية توظيف طرق اكتشاف العلاقات السببية في التطبيقات العملية، خاصة في مجال الرعاية الصحية وعلم الأحياء. وهو يؤكد أن فهم العلاقات بين المتغيّرات يمكن أن يخدم الأبحاث العلمية الأساسية ويساعد في تطوير أدوية جديدة، حيث يقول: “نرغب دائماً في معرفة المزيد حول الصحة والعمليات البيولوجية عند البشر، ولكن هناك جوانب كثيرة ما زلنا نجهلها في هذا المجال”.

لم يكن الفضول الدافع الوحيد وراء تركيز لي على دراسة العلاقات السببية، بل نتج ذلك أيضاً عن تجربة شخصية. فقد كان متخصصاً في هندسة البرمجيات أثناء دراسته الجامعية، ولكنه بعد وفاة أحد أفراد أسرته بسبب السرطان قرّر الانتقال إلى مجال يمكن أن يكون له أثر ملموس في تحسين صحة الإنسان. وهو يوضح ذلك بقوله: “اخترت دراسة العلاقات السببية لأنها إحدى أفضل الطرق لاكتشاف سبب الأمراض”.

الاحتمالية والحتمية

يعكف لي وأمثاله من الباحثين في مجال اكتشاف العلاقات السببية على صياغة ما يُعرف بالرسوم البيانية الموجَّهة، وهي تمثيلات مرئية للعلاقات بين مجموعة من المتغيّرات. وتمثِّل العُقد في هذه الرسوم المتغيّرات، بينما تمثِّل الروابط العلاقات السببية التي تربط بينها.

تُصمّم أُطر اكتشاف العلاقات السببية عادة وفق مبادئ احتمالية تأخذ في الحسبان مستويات من الخطأ. ولكن لي يوضح أن الحياة الواقعية فيها علاقات حتمية وليست احتمالية، بمعنى أن بعض المتغيّرات يمكن أن تُحدَّد بشكل قطعي بناء على أسبابها المباشرة دون وجود أي درجة من الشك.

أحد الأمثلة على ذلك حساب مؤشر كتلة الجسم من خلال صيغة ثابتة هي قسمة وزن الشخص على مربع طوله، مما يعني أن العلاقة بين الوزن والطول ومؤشر كتلة الجسم علاقة حتمية وليست احتمالية، لأنها لا تتأثر بأي انحرافات عشوائية.

والعلاقات الحتمية شائعة في الحياة الواقعية، ولكنها تمثّل تحدياً لأطر اكتشاف العلاقات السببية القائمة على المفاهيم الاحتمالية. لذلك سعى لي وزملاؤه إلى إيجاد طريقة لاكتشاف العلاقات السببية يمكن استخدامها بنجاح في حالة العلاقات الحتمية.

الطرق الشائعة لاكتشاف العلاقات السببية

هناك طريقتان رئيسيتان مستخدمتان حالياً في اكتشاف العلاقات السببية، وهما الطريقة القائمة على القيود، والطريقة القائمة على الدرجات. وربما تكون أكثر الطرق القائمة على القيود شيوعاً هي خوارزمية PC (التي طورها العالمان بيتر سبيرتس وكلارك غلايمور وتمت صياغة اسمها من الحرف الأول من اسم كل منهما). في المقابل، تمثل طريقة البحث الجشع إحدى الطرق الشائعة القائمة على الدرجات.

تُعدّ الطرق القائمة على القيود، بما فيها خوارزمية PC، غير مجدية في حالة العلاقات الحتمية. فعندما تتوافر متغيّرات إضافية ترتبط مع المتغيّرات الأصلية بعلاقات حتمية، يصبح من الصعب تحديد العلاقات السببية. لكن عند ملاحظة مزيد من المتغيّرات المترابطة، ينبغي من الناحية النظرية أن يصبح اكتشاف العلاقات السببية أسهل. من هنا استلهم لي وزملاؤه تعديلاً بسيطاً على طريقة البحث الجشع مكّنهم من تطوير طريقة مفيدة في حالة العلاقات الحتمية.

أطلق الباحثون على طريقتهم الجديدة اسم “البحث الجشع المُراعي للحتمية”، وهي تتكون من ثلاث خطوات. في الخطوة الأولى يحدد الباحث مجموعات المتغيّرات المترابطة بعلاقات حتمية عن طريق استكشاف ما إذا كان بالإمكان تحديد متغيّر معيّن بالاستناد إلى بعض المتغيرات الأخرى. ثم تُنفذ عملية بحث جشع على جميع المتغيّرات بهدف تكوين رسم بياني مبدئي للعلاقات بينها. وفي الخطوة الثالثة يجري الباحث عملية بحث دقيق يقتصر فقط على المجموعات الحتمية والمجموعات المجاورة لها.

تقسّم هذه الطريقة البيانات إلى ثلاثة أنواع: مجموعات حتمية، ومجموعات غير حتمية، ومجموعات وسطى تفصل بين النوعين السابقين. ويشير لي وزملاؤه في دراستهم إلى أن الرسم البياني للعلاقات السببية يمكن تقسيمه بكامله إلى هذه الأنواع الثلاثة.

وقد أجرى الباحثون مقارنة بين طريقتهم (البحث الجشع المُراعي للحتمية) والطرق الأخرى، بما في ذلك خوارزمية PC وطريقة البحث الجشع التقليدية، فوجدوا أن طريقتهم تتميز بأداءً أفضل في عدّة سيناريوهات وفق معايير مختلفة على مجموعة بيانات صناعية. ولكنهم لاحظوا أنه مع زيادة عدد المجموعات الحتمية في مجموعة البيانات، يزداد الوقت اللازم لتشغيل الخوارزمية بسبب زيادة العلاقات التي يجب تحليلها عبر البحث الدقيق، مما يتطلب موارد حسابية أكبر.

مجموعة بيانات حقيقية

طبّق لي وزملاؤه هذه الطريقة على مجموعة بيانات حقيقية مأخوذة من دراسات سريرية وتتضمّن معلومات حول كيفية استقلاب المرضى للأدوية. وشملت تلك البيانات ثلاثة أنواع من المعلومات، وهي خصائص المريض (مثل الطول والوزن)، ومعلومات عن الأدوية (مثل طريقة تناولها والجرعة المستخدمة)، وسجلات القياس التي توضّح مدى سرعة تخلّص جسم المريض من الدواء.

نجحت طريقة لي وزملائه في رصد ثلاث مجموعات حتمية في البيانات، بينما لم تنجح الطرق الأخرى في ذلك. على سبيل المثال، حددت طريقة الفريق العلاقات بين الطول والوزن ومؤشر كتلة الجسم مع الحفاظ على الروابط بين هذه المتغيّرات والمتغيّرات الأخرى غير الحتمية. ويعلّق لي على ذلك قائلاً: “لهذا الأمر دلالة مهمة، حيث تتيح طريقتنا الحفاظ على الروابط المفيدة بين المتغيّرات”. أما في الطرق الأخرى، فإن الروابط بين المتغيرات الحتمية وغير الحتمية تختفي.

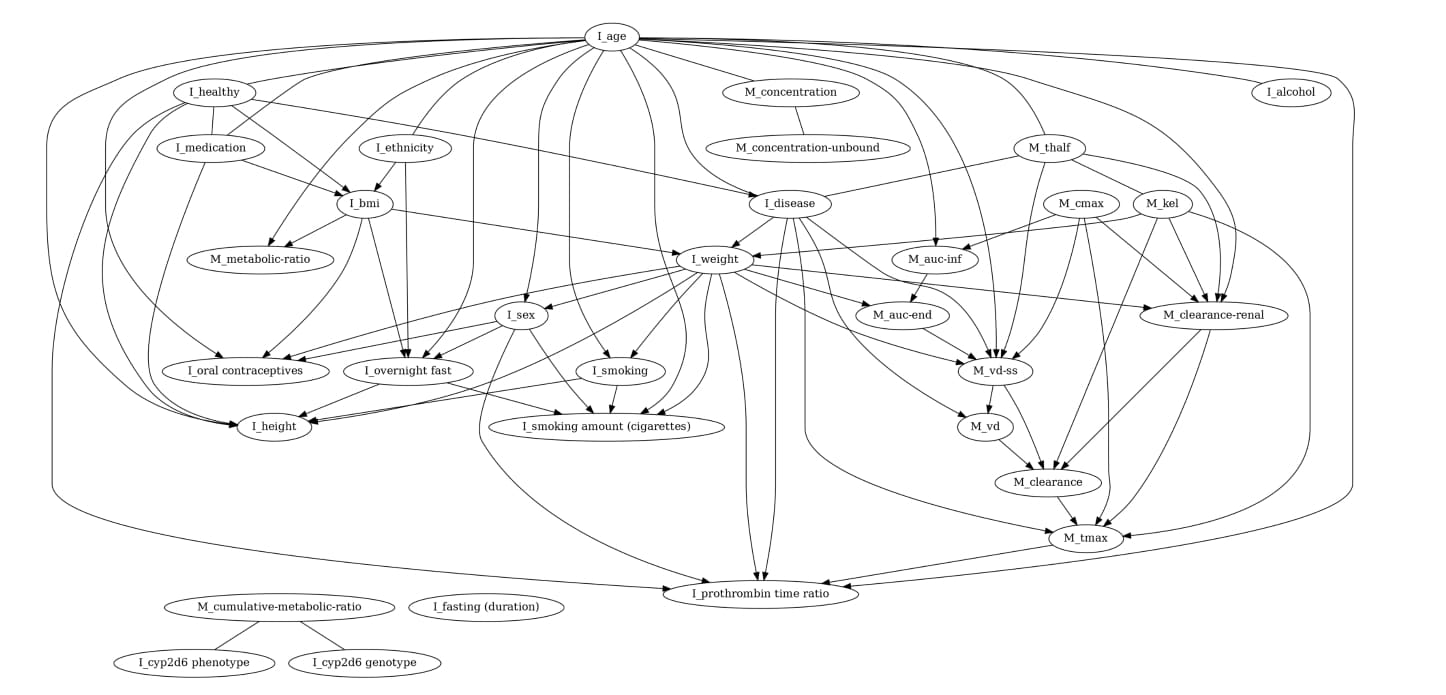
طوّر الباحثون طريقة جديدة لاكتشاف العلاقات السببية تُعرف باسم “البحث الجشع المُراعي للحتمية” بهدف تحديد العلاقات الحتمية وغير الحتمية بين المتغيّرات في مجموعة بيانات واقعية مأخوذة من تجارب سريرية، وهو أمر كان يشكل تحدياً بالنسبة للطرق السابقة.

مشاكل جديدة بحاجة إلى حلول

يأمل لي في أن يتمكن مستقبلاً من تحسين طريقة البحث الجشع المُراعي للحتمية بحيث تصبح قادرة على تحديد المتغيرات الحتمية بشكل كامل من خلال زيادة عدد الافتراضات.

كما يشير إلى أنه على الرغم من تمكنه مع بقية فريقه من حل إحدى المشاكل المتعلقة بتحديد العلاقات الحتمية في البيانات الحقيقية، فهناك الكثير من المشكلات الأخرى التي ما زالت تنتظر حلولاً، من بينها الصعوبات المتعلقة بأخطاء القياس، وهي شائعة في مجموعات البيانات الحقيقية.

وفيما يتعلق بالخطوات التالية، يقول لي إنه ينظر في كيفية دمج الأفكار الناتجة عن تطوير طريقة البحث الجشع المُراعي للحتمية مع طرق جديدة لمعالجة أخطاء القياس، مؤكداً أنه: “يمكننا الجمع بين عدة تحدّيات والنظر في كيفية إيجاد حل لها في مجموعات البيانات الحقيقية”.